Preface
Through my Prolegomenon, I am attempting to create a «transcendental method» which is arrived at from self-evident axiomatic truths (‹truth› with lowercase t) of mathematics and de-ontologized without a necessary background ontology (for examples of «background ontologies» see how the realm of the virtual supports the realm of actuality in Gilles Deleuze, or how the ‹ontic› is supported by the ‹ontological› in Martin Heidegger). Ultimately, I am interested in a ‹methodological dualism› between the ‹manifest image› of ‹being-in-the-world› (culture, the arts, politics, human affairs, soft sciences) versus the ‹scientific image› of the exact sciences. These two domains are incommensurable with each other. But more on that later. Cultural analysis is of the former realm and theoretical science is of the latter realm. Culture can never be as exact as science, but science is developed posterior to culture. But culture depends on science for «first principles» that undergird «reality.» For more on the distinction between the manifest image and the scientific image:
«Philosophy and the Scientific Image of Man» (PSIM) describes what Sellars sees as the major problem confronting philosophy today. This is the «clash» between «the ‹manifest› image of man-in-the-world» and «the scientific image.» These two ‹images› are idealizations of distinct conceptual frameworks in terms of which humans conceive of the world and their place in it. Sellars characterizes the manifest image as «the framework in terms of which man came to be aware of himself as man-in-the-world,»[0] but it is, more broadly, the framework in terms of which we ordinarily observe and explain our world. The fundamental objects of the manifest image are persons and things, with emphasis on persons, which puts normativity and reason at center stage. According to the manifest image, people think and they do things for reasons, and both of these «can occur only within a framework of conceptual thinking in terms of which [they] can be criticized, supported, refuted, in short, evaluated.»[1] In the manifest image persons are very different from mere things; things do not act rationally, in accordance with normative rules, but only in accord with laws or perhaps habits. How and why normative concepts and assessments apply to things is an important and contentious question within the framework.
The manifest image is not fixed or static; it can be refined both empirically and categorically. Empirical refinement by correlational induction results in ever better observation-level generalizations about the world. Categorial refinement consists in adding, subtracting, or reconceptualizing the basic objects recognized in the image, e.g., worrying about whether persons are best thought of in hylomorphic or dualistic categories or how things differ from persons. Thus, the manifest image is neither unscientific nor anti-scientific. It is, however, methodologically more promiscuous and often less rigorous than institutionalized science. Traditional philosophy, philosophia perennis, endorses the manifest image as real and attempts to understand its structure.
One kind of categorial change, however, is excluded from the manifest image by stipulation: the addition to the framework of new concepts of basic objects by means of theoretical postulation. This is the move Sellars stipulates to be definitive of the scientific image. Science, by postulating new kinds of basic entities (e.g., subatomic particles, fields, collapsing packets of probability waves), slowly constructs a new framework that claims to be a complete description and explanation of the world and its processes. The scientific image grows out of and is methodologically posterior to the manifest image, which provides the initial framework in which science is nurtured, but Sellars claims that «the scientific image presents itself as a rival image. From its point of view the manifest image on which it rests is an ‹inadequate› but pragmatically useful likeness of a reality which first finds its adequate (in principle) likeness in the scientific image.»[2] Is it possible to reconcile these two images? Could manifest objects reduce to systems of imperceptible scientific objects? Are manifest objects ultimately real, scientific objects merely abstract constructions valuable for the prediction and control of manifest objects? Or are manifest objects appearances to human minds of a reality constituted by systems of imperceptible particles or something even more basic, such as absolute processes (see «Foundations for a Metaphysics of Pure Process»)? Sellars opts for the third alternative. The manifest image is, in his view, a phenomenal realm à la Kant, but science, at its Peircean ideal conclusion, reveals things as they are in themselves. Despite what Sellars calls «the primacy of the scientific image,»[3] he ultimately argues for a «synoptic vision» in which the descriptive and explanatory resources of the scientific image are united with the «language of community and individual intentions,» which «provide[s] the ambience of principles and standards (above all, those which make meaningful discourse and rationality itself possible) within which we live our own individual lives.»[4], [5]
My hope with the Prolegomenon is to create an autonomous free-standing axiomatic system derived from synthetic judgements. But ultimately, we are faced with the problem of reconciling these two registers, cultural and scientific. My Prolegomenon articulates the a priori of the subject which is a universal condition of possibility to empirical experience. The phenomenological experience of the subject is bracketed into neuro-geometric or cognitive definitions of the subject. These soft sciences are of the realm of the manifest image. The scientific image is the realm of intensional mathematical systems, which is exact yet de-ontologized. It need not prove existence! Category theory is intensional. Homotopy type theory is intensional. There need not be a background ontology to support such intensional statements. The exact rigor of these systems is arrived at hypothetico-deductively. The intensional statements need not postulate the existence of its statements. For example, one need not posit the existence of the number 2, but one can intensionally define 2 + 2 = 4 and it is true by way of the axioms. For more on the distinction between intensional and extensional statements:
For example, an intensional definition of the word ‹bachelor› is ‹unmarried man›. This definition is valid because being an unmarried man is both a necessary condition and a sufficient condition for being a bachelor: it is necessary because one cannot be a bachelor without being an unmarried man, and it is sufficient because any unmarried man is a bachelor.
This is the opposite approach to the extensional definition, which defines by listing everything that falls under that definition—an extensional definition of ‹bachelor› would be a listing of all the unmarried men in the world.
As becomes clear, intensional definitions are best used when something has a clearly defined set of properties, and they work well for terms that have too many referents to list in an extensional definition. It is impossible to give an extensional definition for a term with an infinite set of referents, but an intensional one can often be stated concisely—there are infinitely many even numbers, impossible to list, but the term ‹even numbers› can be defined easily by saying that even numbers are integer multiples of two.[6]
But as we’ll see, homotopy type theory proves the existence of all its statements constructively (Curry-Howard correspondence). So, these are not fictitious objects! Constructive intuitionistic type theory allows us to demonstrate existence through the invocation of a particular ‹token›. Every constructive proof has a witness of the construction. We are building in real time in homotopy type theory.
Now, the manifest realm of ‹being-in-the-world› could be postulated elegantly by way of neuroscience/cognitive science/experimental psychology which ultimately depends on computational neuroscience, the latter of which is expressed in its purest form by a rigorous mathematical system undergirding the extant logic of the applied (psychological) realm. Applied math vs. pure math… more or less! My Prolegomenon is attempting an exact science of the philosophy of being and structure through the questions of the foundation of mathematics and its ontology.
Now as an artist, my activity (of the cultural realm… or the manifest image) can interact with such an exact science (the scientific image) through what Wilfrid Sellars calls the «synoptic vision.» In the cultural sphere, I am aiming for a ‹total work of art› with my artistic activity, which incorporates emotional intimacy and radical transparency into the work itself through multiple modes of expression (the genres of painting, sculpture, poetry, sound, techno, computer music, art criticism, etc.) and interdisciplinary erudition (knowledge of Fluxus, sound poetry, noise music, contemporary art, philosophy, disco music, etc.). Now here is the corollary of what I have said: If one were to read my artistic activity without this scientific image, which is the exact science which undergirds all of my cultural activity, one would grossly misunderstand the full extent of my artwork.
The most important tool to the understanding of my Prolegomenon is Reza Negarestani’s articulation of navigation between the ‹local› and the ‹global›, which is central to mathematics. Negarestani is summarizing the ideas, for example, of Jean Petitot, René Thom, Albert Lautman and Guerino Mazzola in this mathematical notion:
What French mathematician and philosopher Jean Petitot calls ‹bimodalization› in mathematics is the unfolding of a generative synthetic environment between modal poles and for that purpose what is needed is a rigorous program to generalize concepts procedurally, or in other words, bimodalize them into their particular and general modes, local and global constructs.[7] There is a long trajectory of historical conceptual and philosophical problems behind this generalizing program of today’s mathematics. It is not as if mathematics has some kind of obsession with generalization—no, these are responses to certain historical problems of philosophy and, in a more particular sense, mathematical problems that have been arrived at and which now mathematicians are working on. The generalization aspect of mathematics and the idea of bimodalization that facilitates the generativity of mathematics brings us back to the subject of this topic which is the formalization of the space of the universal and a robust identification of a local site as immersed in this space.
I start the question of ‹approaching the space of the universal› by discussing the problem of localization. Reductively speaking, in order to approach a space whose full scope is not given, we need to start somewhere, which is to say, we need to find and identify a site through which we can approach this space without ever overstretching the resources of the site or being restricted to the immediate resources of its local horizon. This is the question of localization, which I believe is one of the most classical problems of philosophy. In fact, the question of localization undergirds the kind of ontological and epistemological justification you make about yourself, the subject and the world. Precisely because it is the localization that permits a robust approach and it is the robust approach—in the sense of navigation of different pathways—that forms knowledge and makes sense of ontology. Localization is always an act of organization or configuration, it operates under the schema of ‹doing violence› to a landscape as Gilles Châtelet suggests.[8] A perturbation, the injection of disequilibrium, a designated alienation, a systematic distancing that brings about the possibility of qualitative organization of information from homogenous information where nothing is given.[9]
Introduction
«If I live on a surface, the world no longer faces me; and alterity is no longer lived as a confrontation.»
Gilles Châtelet as quoted by Vera Parlac
I think the classical post-Marxist analysis of the world is too parochial. It is predicated on the State and the unaccounted marginalized identity which has «no identity» within the State’s imposed order of things/accounting apparatus. A good example is when a judge asked Louis Auguste Blanqui about his profession. Blanqui cheekily responded that he was a «proletarian,» only to be dryly reminded that «that is not a profession.» Defining your political practice in response to the hegemonic power structure is reactive, I believe. Similarly, the limits of modernism showed us that any formalizable logic which could be encoded with an arithmetic was incomplete. I remember once having an argument with Jonathan Gean where he said that if I was a formalist, I would necessarily be limited to the closed permutations of a chess board. Connor Camburn recently brought up Marcel Duchamp’s figuration of the chess board. I remember from my Conceptual Art class the classic Duchamp work of three stoppages, which consists of three different means of demarcating a ruler or distance. If one were to get Heideggerian, one could think that any technology or framework inherently enframes (ineffable) Being into some methodological construction which determines our relationship to the world through a predetermined ready-to-hand and methodology. Enframement is the means by which technology, which by way of its mere technical expression is merely material or matter, endows being with a technics. The incompleteness of any system points to the way in which any axiomatizable system has an aporia, which suggests the potential equiconsistence of infinitely many different frameworks for postulating some type of encoded language, which supplicates some accompanying metalanguage. But the problem with dissecting and deconstructing the power or privilege of the identities empowered by the State, is that the argument necessarily reacts to a political reality, which is contingent upon machination and history written by the victors. Even a historiography is limited by way of this dissection of a causal chain of events which merely occur within one register of time, the dominant historical mode which is inherently imperialist, patriarchal, etc.
An alternative means for considering formalism would be to continue the project first initiated by David Hilbert, by means of attempting to find a foundational system for geometry (Grundlagen der Geometrie) as opposed to the Fregean project of a foundational system for arithmetic (Grundlagen der Arithmetik). Only recently, with the work of topos theory from the 1960s–1970s and homotopy type theory after the work of Vladimir Voevodsky and Steve Awodey in 2000s–2010s, do we have an inherently geometric, or should I say topological, means of considering first principles. Rather than building a set-theoretical empire based on a history of antinomies, one is building a type-theoretic system predicated on weak equivalences of homotopic paths. So as opposed to the atomistic framework of propositions with the stricter sense of equality in set theory (i.e., double containment) one is building a constructive system which is based on an intuitionistic type theory which always necessitates a witness (as the proof) to the invocation of any construction (refer to the Curry-Howard correspondence). A foundation of mathematics based upon topology is much more generative, as opposed to the modernist project of a chess board. The weak equivalence of any two paths in the homotopic sense provides an inherently spatial/intuitive sense for any axiomatic method and its resulting conclusions, forming a freestanding autonomous structure. G.H. Hardy said that pure math was aesthetics and such a self-evident hypothetico-deductive method for proving an extant logic upon the world we already intuitively understand is finally the reprise of Hilbert’s formalist project of a system generated from the first principles of points, lines and spaces. Finally, the dream of Nicolas Bourbaki has been achieved by way of category theory. Thanks to Claude Chevalley, who insisted that Bourbaki consider category theory avant la lettre: «Chevalley was a member of various avant-garde groups, both in politics and in the arts… Mathematics was the most important part of his life, but he did not draw any boundary between his mathematics and the rest of his life.»[10]
This Prolegomenon will examine the possibility for a foundational system which conceptually unifies ordinary mathematics (category theory, topos theory, or homotopy type theory are the options) or if we should pursue a constructive intelligence/computationalism instead. For that matter, this treatise will discuss structure in the sense of philosophical structuralism (not to be confused with French Structuralism) and whether category theory provides a structuralism as Awodey suggests. Recent research after the Univalence axiom has demonstrated a new contender: does homotopy type theory provide a foundation for mathematics or is it not important to be a foundation, as Awodey suggests, which would challenge us ontologically to pursue the constructivism of Martin-Löf type theory? We will borrow Negarestani’s notion of ‹localization› and try to provide a more rigorous context for a ‹site› directly within topos theory, which has ramifications for any ontological framework. Moreover, we will discuss the necessary background ontology to any foundational ‹topos› which will depend on the use of the Tarski axiom.
We will address the issue of the ‹synthetic a priori› and whether we can, in the Kantian manner, treat geometry as the ‹a priori›, either at the macro-level, as Albert Einstein has shown, where the Minkowski spacetime develops a ‹spacetime› where the only invariant is the speed of light; or on the meso-level, «the relativity of simultaneity» where «distant simultaneity—whether two spatially separated events occur at the same time—is not absolute, but depends on the observer’s reference frame»;[11] or on the micro-level (of neurons) where perception uses a cut loci which is a geometric form (from differential geometry), so that we can develop a «neurogeometry of vision,» as in the work of Petitot.
Furthermore, we will attempt to articulate some ‹self- evident structural Truth› on the ‹conceptual level› itself. In support of the conceptual level of any epistemology, I will be arguing for a de-ontologized metaphysics to accommodate the ineffability of the Real and the potentia of the conatus (as in Gottfried Wilhelm Leibniz or Baruch Spinoza), but rather than philosophize this ontology through some transcendent background (the realm of ‹virtuality› in Deleuze or ‹the ontological› for Heidegger), we shall wish to view logico-deductive abstraction itself (like in group theory) as a means to articulate intrinsic invariants of material which need not be embedded in a surrounding Euclidean space for its measurement a.k.a. thinking (see Gauss’s Theorema Egregium). Through this immanent hypostatization of material which scientifically determines its own place/count reflexively (in the super-structuralist sense of Louis Althusser, Jacques Rancière or Alain Badiou) but is, simultaneously, completely hypothetical (since it is derived from axioms), one can consider an intensive definition that is completely relative (Alexander Grothendieck’s perspective) which allows for ontological involvement, yet suspends its own background ontology through the complementarity of the duality (François Laruelle) between ‹theorem› and ‹axiom› (or for that matter, between ‹actual› and ‹virtual›). This Laruellean approach may be likened to eliminative structuralism, where «statements» get regimented/deflated into analytic propositions which are trivially/vacuously true for a system through assuming the hypothetical hypostatization of the theory. Because of the vacuity of any deflated statement, this approach flattens the underlying ontology of a philosophical theory through a quantifier parameter beforehand. I will discuss the presuppositions of Time that are based on a real-valued function which is parameterized and argue against ‹the time of philosophers›.
We will still attempt to demonstrate the underlying ontology of ‹technique› charting from the father of individuation Gilbert Simondon; to the Deleuzian system of becoming from the Idea («The Ideal Synthesis of Difference» in Difference and Repetition); to Laruelle’s de-ontologized material experimentation uni-lateral to the Real; to Thom’s discussion of the aporia of the technical opposition between continuity and discontinuity. The de-ontologized metaphysics of Laruelle, which is axiomatically derived (as opposed to a theological doctrine or philosophical transcendence) is explained here:
Philosophers, Laruelle insists, do not know what they are doing. They are never doing what they say or saying what they are doing—even and especially when they purport to be able to legitimate their philosophical decisions in terms of some ethical, political or juridical end. The theoreticist idealism inherent in decision is never so subtle and pernicious as when it invokes the putative materiality of some extra-philosophical instance in order to demonstrate its ‹pragmatic worth›. To condemn Laruelle for excessive abstraction on the grounds that the worth of a philosophy can only be gauged in terms of its concrete, extra-philosophical (e.g., ethical, political or juridical) effects is to ignore the way in which extra-philosophical concretion invariably involves an idealized abstraction that has already been circumscribed by decision…
In non-philosophy, radical axiomatic abstraction gives rise, not to a system or doctrine inviting assent or dissent, but to an immanent methodology whose function for philosophy no one is in a position to evaluate as yet. Ultimately, then, non-philosophy can only be gauged in terms of what it can do. And no one yet knows what non-philosophy can or cannot do.[12]
At the level of physics, an Aristotelian realism makes the most sense, which is known in the sciences as «ontic structural realism.» Why? Epistemology, at the level of structure, is either «in the thing» realism, «before the thing» Platonism or «after the thing» eliminative structuralism.[13] If one is of the realist camp, one would say that relativity exists in situ on the macro scale of large bodies, but that these structures don’t appear in everyday life due to a scale problem. Similarly, catastrophic hysteresis means there is a lag between those infected with the SARS-CoV-2 virus between one week and the next, but only when a pandemic does in fact occur. But can we accept the entities described by physics as actually existing? Certainly it is true that special relativity is true as a framework. But as Negarestani has explained, Bas van Fraassen did not believe electrons really existed.[14] Negarestani has previously articulated an ontology defined by epistemology, which is not reducible to mere «ontological monism.» We will counter that categorical-structuralism provides the basis for a variant form of realism that is similar to «set-theoretic structuralism,» where «structures are isomorphism types (or representatives thereof) within the set-theoretic hierarchy.»[15] But the ontological commitments of such a system need not presuppose a «rich ontology of sets.»[16] The question still remains if category theory is isomorphism invariant. It is! But one could consider topos theory instead. But there is still the question of Grothendieck universes needed for topos theory. We will not be able to rigorously consider the ontology of topos theory unless we consider the Tarski axiom which presupposes an inaccessible cardinal (i.e., infinity). But, for example, Andrew Wiles in his proof of Fermat’s Last Theorem did not need to even invoke these uncountable universes. The solution I believe to this foundational problem would be to pursue inquiry into a (more contemporary) field known as homotopy type theory, which views things as instances, known as ‹tokens›.[17]
Does the recent work in category theory present an argument for structuralism, as a completely top-down (by its intensional nature) approach to math (as opposed to bottom-up constructions) or should we pursue the constructive computationalism of homotopy type theory? The «ontic structuralist realist» James Ladyman has suggested homotopy type theory is a foundation for mathematics.[18] Awodey has said it provides a philosophical structuralism.[19] Other examples of this notion of top-down classification in mathematics include Gaussian curvature (which is an invariant for different types of elliptic, hyperbolic, or Euclidean geometry), Klein’s group-theoretic program of non-Euclidean geometry (which are group invariants, such as cross ratio, for different types of affine or projective geometry), and category theory. This top-down organization of mathematics presents a multiplicity of ‹case(s)› through general ‹invariants› (topological, group-theoretic or categorical) which constrain the (group-theoretic or categorical) objects into varying geometries (Klein’s method) or algebraic structures (category theory).
The «highest truth,» to build off Alexander Boland’s point about «craftsmanship,» follows what he calls intuitive compositionality or Spinoza’s intuition. In a categorical context, objects are literally only unique «up to isomorphism» and morphisms are the generalizing tool, which leads back to the question of «the conceptual level» mentioned before.[20] To qualify an idea by Boland where he states «I believe everything is a matter of aesthetics simply because all of epistemology is autopoietic,»[21] I would counter with «everything is a matter of aesthetics since all epistemology is conceptual. Conceptual mathematics and the axiomatic method are geometric. Therefore, everything, by way of epistemological delimiters, is a matter of aesthetics.» This is «conceptual poetry» (from the axioms) as opposed to «autopoiesis»; because instead of a homeostatic system (in the case of Niklas Luhmann and the imperfect model), there is a sense of «sheen» in the multivariate calculus of a manifold in which the «geometric intuition» is pure, as if pre-constituted. Pure mathematics is a matter of aesthetics according to the mathematician Hardy in A Mathematician’s Apology. I am not arguing for Platonic Forms but rather for some form of Aristotelian realism, where logic and geometry converge, and that structure takes place in exact terms within the Real itself but requires hypothetical actualization to confirm, such as the thought-experiment of Einstein’s special relativity. There is no universal truth in the heavens. The Real is a necessary cause but the actuality need only be sufficient and not directly manifest (de-actualized worlds that have a unilateral source, the Laruellean Real). The conceptual invention of topological machinery, for example in a topos, allows for radical approaches between knowing subject and the ostensibly fixed object. ‹Base changes› allow for the freedom to move from one level of ‹open sets› to another in the navigation of a topos. The invention of this conceptual machinery which formalizes intuition at the highest level of abstraction is novel for «unify[ing] deep insights on arithmetic (number) and geometry (form).»[22] The conceptual invention of the epistemologically unmoored geometry, from the wellspring of the individuation/ontogenesis, is a becoming. These ‹germs› (in a ‹section› of a ‹stalk›) are «salient forms» which have been individuated from the «pregnance» emanating from «source-forms» (to use Thom’s words from Semio Physics). This is morphogenesis, of the realm of aesthetic creation, individuated through germs of a ‹sheaf›. Dynamic perspectives. But through the axiomatic nature of such a geometry, we hope to defend a de-ontologized metaphysics that is not an «abusive hypostasis.» The axiomatic method allows for pure aesthetic fabrication (in the sense of Hardy), but one that is freestanding and geometric, as opposed to Gottlob Frege’s schematic assertion of God.
In imperfect cases, such as Luhmann’s autopoietic systems (social or dynamical), these predictive determinisms have outliers which aren’t predicted. The question ultimately remains whether or not all systems beyond thermodynamics (such as economics, for example) are ergodic? Boland has made the point in conversation that cybernetics is not ergodic. This is all to suggest that at a deeper level, there are cases when systems abide by larger «extant forms» and are not simply reducible to the recalibration of a system (predictions which only hold in 99.99% of cases, which is why there are outliers such as the Great Depression). That is, there are forms which are algebraically precise in a geometric/topological sense (for example, see topological invariants such as compactness, that every open cover has a finite subcover) and are therefore, more intuitive. We could take an economic space and ask if it is convergent. If it is metric, then the space will be compact when it is complete and totally bounded. So, if we can locate some upper bound for the supply and demand, and if all the limits are contained in the metric space, then it would be complete. So the value of a product (in economics) may follow some heuristic such as the «law of diminishing returns,» but this is only a principle and not naturalized since how can we define the topology of the space of utility (in the same sense, Moore’s law is not exact in a mathematical sense either). Some truths exist in their algebraic exactness of terms, which can’t be simplified to the heuristic of a system. One example is generalizing basic arithmetic to a topos wherein logic becomes inherently geometric. According to Alain Connes and Caterina Consani, one can think of the integers as geometric through the semiring of tropical integers as a sheaf of sets over a topos.[23] The case of the logic of catastrophe modeling or Monte Carlo simulation, which is the ‹autopoietic›, is prone to ‹error› and different from the more precise geometric formalism, that is still axiomatic.
At the formal level (in the manner of Hilbert’s formal system for geometry), eliminative structuralism for categorical structuralism or what Elaine Landry calls ‹semantic realism›, which is ‹schematic› as opposed to ‹assertoric›, makes the most sense epistemologically, in the sense that objects can be viewed from the exterior rather than interior, through the categorical approach: all that matters is «arrows only» (morphisms between objects). The meaning of category theory can be understood intensionally. I will conclude the Prolegomenon with a postscript which discusses the social sciences and the mathematical presuppositions of cybernetics/economics which are problematic. For example, a Java program would not be able to compute certain functions due to uncountability. We therefore suggest to the reader interested in an alternative ontology (to this problematic one) to pursue the ontology advocated by Diedrich Diederichsen in his «Intimacy and Gesamtkunstwerk» in Kai Kein Respekt (predicated on «homosociality»).
I. Topos through navigation between the local and global
All this work culminated in another notion, thanks to Grothendieck and his school: that of a topos. Even though toposes appeared in the 1960s, in the context of algebraic geometry, again from the mind of Grothendieck, it was certainly Lawvere and Tierney’s (1972) elementary axiomatization of a topos which gave impetus to its attaining foundational status. Very roughly, an elementary topos is a category possessing a logical structure sufficiently rich to develop most of «ordinary mathematics,» that is, most of what is taught to mathematics undergraduates. As such, an elementary topos can be thought of as a categorical theory of sets. But it is also a generalized topological space, thus providing a direct connection between logic and geometry.[24]
The foundational problem since Kurt Gödel’s Incompleteness Theorem is whether any formal system is complete and/or inconsistent. A system is complete if «all truths expressible in Σ are theorems.»[25] A system is inconsistent wherein both P and Not-P are proven to be true. Moreover, the Peano Arithmetic (derived from the Peano axioms), if it is consistent, cannot prove its own consistency. This proof is shown by «translating the workings of Turing machines into arithmetic.»[26] Kripke-Joyal semantics has been shown to be complete. Kripke-Joyal semantics views propositions as true within possible worlds:
The basic idea of the semantics is that a proposition is necessary if and only if it is true in all «possible worlds.» The idea is made precise as follows:
A Kripke frame is a set W, the elements of which are called possible worlds, together with an accessibility relation R, that is, a binary relation between elements of W. A Kripke frame becomes a Kripke model when a valuation is given. A valuation val takes a world w and an atomic formula P and gives as value 0 or 1, to determine which atomic formulas are true at what particular worlds.[27]
Each reference frame provides a truth value of whether the atomic formula is true in such-and-such world.
What is most interesting about this «possible worlds» semantics is its use within topos theory.
As part of the independent development of sheaf theory, it was realized around 1965 that Kripke semantics was intimately related to the treatment of existential quantification in topos theory. That is, the ‹local› aspect of existence for sections of a sheaf was a kind of logic of the ‹possible›. Though this development was the work of a number of people, the name Kripke–Joyal semantics is often used in this connection.[28]
Topos theory uses an intuitionistic Kripke logic and can be visualized according to Figure 1.
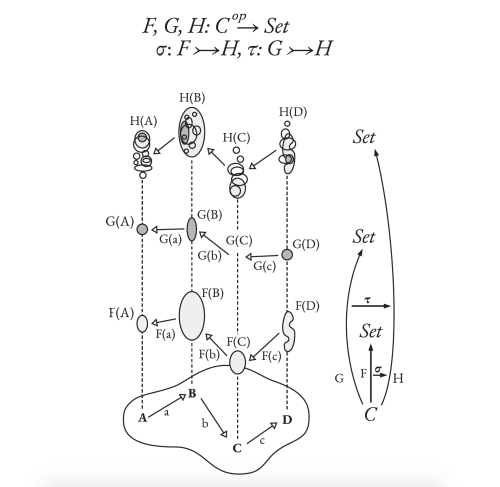
Fig. 1 Topos of variable sets
Each ‹stalk› (i.e., vertical line) over A, B, C, D, in C has a ‹germ› at various levels, i.e., the circles at the different levels; these are ‹sets› above the ‹site›. Here is the definition of a topos:
[O]ne can also find three fundamental concepts in Grothendieck’s toposes: at the base, the Grothendieck topology J in an adequate category C and its associated site (C, J); at the approximation level, a collection of sheaves with its gluing properties; at the ideal level (or point at infinity), the emerging complete structure of the topos with its limits, exponentials, and classifier object.[29]
We can begin to dissect what a topos is, it is a «category of sheaves of sets on a site C»; for a more precise exposition of a topos and the Grothendieck topology in more general cases, see footnote.[30]
Fernando Zalamea, philosopher of math, explains:
In a similar vein, Grothendieck toposes (categories equivalent to categories of sheaves over abstract topologies, 1962) constitute plastic sites, specifically open to dynamic variations. Grothendieck toposes unify deep insights on arithmetic (number) and geometry (form). Beyond Cantorian, classical, static sets, the objects in a topos are to be understood as generalizations of variable sets [see Figure 2]. Instead of living over a rigid bottom, governed by classical logic, they live over a dynamic Kripke model, governed by intuitionistic logic. Beyond the classical example of the separated sheaf of holomorphic functions, a sheaf does not have to be separated in a general topos: points do not have to determine their associated objects. We can even imagine objects without points, defined only through flux processes. A wonderful example is the topos of actions of monoids. Such a topos has an underlying classical logic (where the law of excluded middle holds and points are essential) if and only if the monoid is a group. Thus, when we deal with structures which are monoid non-groups, the logic of their action is just intuitionistic, non-separated, closer to topological fluxions, deformations, disruptions.[31]
One can think of sheaves as follows. Here is a «visualization of a sheaf in terms of stalks over each point of the space»[32]:
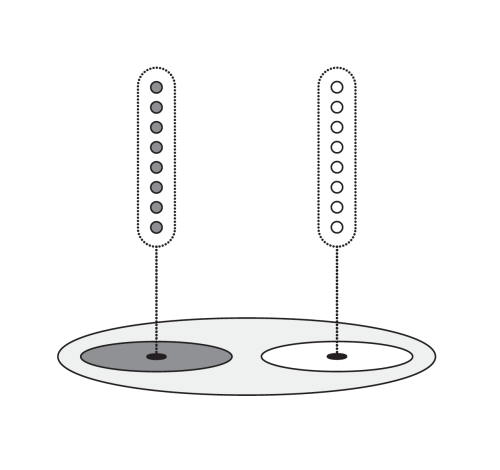
Fig. 2 to 4 Sheaves with sections, germs and gluings
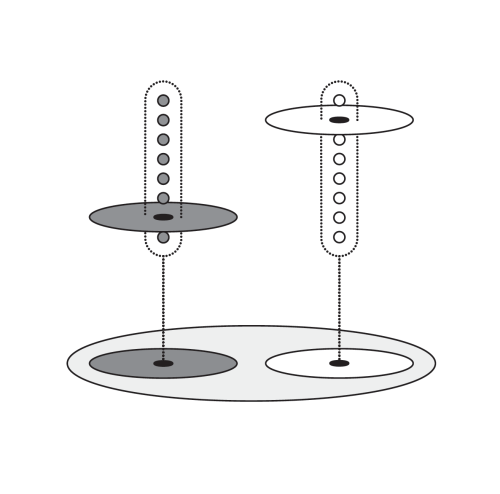
Next, one can take «particular sections (associated to a germ of the stalk) corresponding to each of the dark gray and white open sets of the space.»[33]
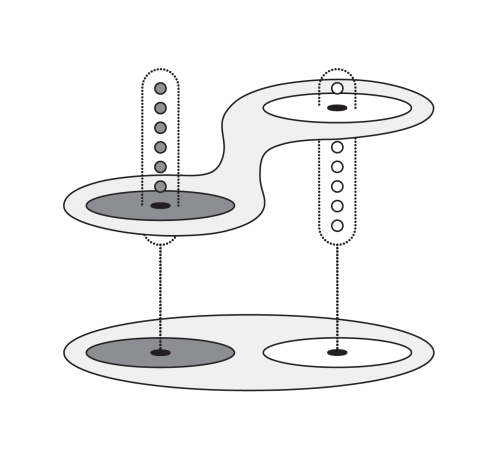
Then, one can «glue together two sections to create a section of the larger open set that they provide a cover of.»[34]
This is a radical breakthrough in the way one can view objects in an epistemological sense. The conceptual breakthroughs of topos theory are insinuated in Negarestani’s essay «Where is the Concept?» on localization. Negarestani even uses the terminology of ‹site› and ‹topos› at times in the essay. One of the primary methods of epistemology in this Prolegomenon will be modeled on this approach of the localization of the concept, which Negarestani characterizes by its epistemological depth to «unmoor» the subject from fixed points and «cancel» any archetypal relation between subject and object, immersing the subject directly within the «navigational landscape»:
Just like the desert that is one and the same and precisely because of its homogeneity we don’t have access to its landscape, the monism of nature does not allow us to know nature without organizing an epistemic breakage. Ontologically, nature does not distinguish itself from itself. Monism is in this sense an ontological reality that demands a necessary epistemic strategy: Exactly because of this excess of informational homogeneity—a desert that is one and the same everywhere—we can’t immediately approach nature or navigate it. The nature-culture division is an epistemic division, not an ontological one. From the possibility of epistemic traction, this division is necessary and far from rigid. It provokes approaches to nature hitherto unimagined. To claim that everything is nature is at best an indulgence in the vulgarity of the obvious and at worst, a complete blindness to the epistemic conditions through which we are able to progressively make sense of nature.
The bimodalization of the universal to its global and local horizons is a navigational strategy which must be conceived through a local rupture, a regional discontinuity. To create or conceive this local rupture is the basic gesture behind the formation of the concept as a local site distinguished by its qualitatively differentiated information. It is the concept as a regional breakage or local disturbance in the qualitatively homogenous information that provokes approaches and pathways impossible in the absence of the epistemic rupture. Trying to understand nature without an epistemic division, solely through the ontological monism, is an appeal to mysticism. It results either in an ineffable conception of nature or an image of nature as a reservoir of meanings and stories about itself. Once we insist that the world is a repository of meanings, that it has stories to tell the subject without any demand for the subject to create a necessary epistemic condition, then we have already committed to conserve a stable relation between the knowing subject and the world. The world is always facing the subject as if it wants to tell a story, there is no need for the subject to destabilize its given status, to epistemically uproot itself so as to procedurally navigate the landscape. The subject of the world as a ready-made object of experience and a reservoir of meanings is quite stubbornly an anthropocentric and conservative form of subject even though it claims to be completely the opposite.
Localization should be understood in terms of bringing about an epistemic condition that once rigorously pursued cancels any conserved relation between the knowing subject and the world, rather than anchoring the subject in any specific place, it unmoors the subject within a navigational landscape. This is the deracinating effect that registers itself as a condition of enablement insofar as it liberates epistemic possibilities which until now had remained captives of the tyranny of here and now—that is, the knowing subject tethered to a local domain and a privileged frame of reference. Localization has obvious implications for thought not only because we ourselves are local instantiations within the terrestrial horizon, but also from an epistemological perspective: the concept as the space through which we gain traction on the world is a local horizon. As the most fundamental unit of knowledge, the concept is a local horizon, a locally organized space of information within a vast inferential economy and immersed within the general structure of knowledge. So the question of localization allows us a form of systematic study of the local context, and in particular a systematic analysis of conceptual behavior. In this sense, we can say that localization is the ultimate procedural framework of thought. It’s a procedure—even a gradualist and stepwise procedure—because, as I shall argue, the local is not rooted. Its analysis is not a matter of zooming in and out on a specific point. Instead the examination of the local requires a procedure to follow it in a navigational context, in relation with other local horizons, via different directions and addresses. No axiomatic commitment at the level of the local makes sense unless through this procedure, which is to say, only when we localize parameters and orientations or generally speaking identify what makes a local domain local. The local is not a fixed point in space, it is a mobile framework immersed within a generic environment. Its internal analysis is always coupled with an external synthesis.[35]
To get a sense of what Negarestani exactly means by ‹localization›, one would need to familiarize oneself with the work of Thom. The assertion that «the bimodalization of the universal to its global and local horizons is a navigational strategy which must be conceived through a local rupture» is a direct allusion to Thom. Thom was famous for his catastrophe theory where a local rupture creates an epistemological breakage in the fabric of homogeneous information. Catastrophe theory was thought to be a method for predicting catastrophes but the applications of the field proved to be not so fruitful. But the largest import the field had on mathematics was Thom’s invention of the term «attractor,» which would be important in the field of chaos theory. One of the main reasons predictions and applications were not obtainable was that Thom’s approach was completely topological and was an analogical hermeneutics of data and therefore a qualitative study of quantitative data. The motivation of this approach was to undertake a natural philosophy project which could unify the body and soul into a geometric object.[36] To get a better sense of the procedure of localization, we will examine one of the seven elementary catastrophes which Thom describes:
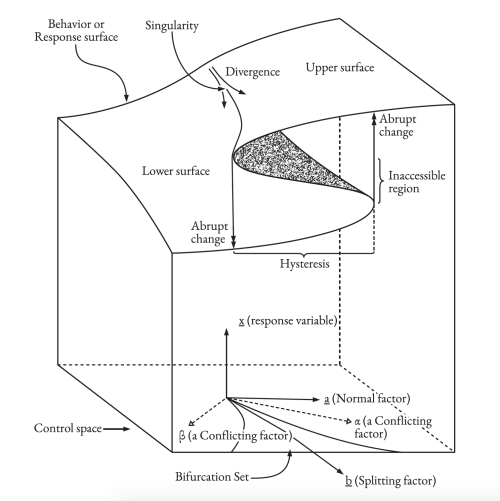
Fig. 5 Cusp catastrophe
This example is known as the ‹cusp catastrophe›. Here a local rupture creates a sudden jump between the upper stable region and the lower stable region. For Negarestani, this divergence creates the possibility, through epistemology, of grasping the problematic ontology of a monist space. In the picture, as the x and y coordinates change in the cusp region, the z coordinate is very unstable (an example of a catastrophe would be a hurricane). Pictured is what is known as hysteresis or a lag between one state and the next state. A good example of hysteresis (a lag) in general would be the number of cases of SARS-CoV-2 virus between one week and the next week, where the number of cases detected grows as new testing detects newer cases. As Anthony Fauci states, «[w]hen you are dealing with a virus outbreak, you’re always behind where you think you are.»[37] A true example of a catastrophe is «the change in shape of an arched bridge as the load on it is gradually increased. The bridge deforms in a relatively uniform manner until the load reaches a critical value, at which point the shape of the bridge changes suddenly—it collapses.»[38] The key to localization is the liberation of the subject from the tyranny of a fixed point or moment or perspective. As Negarestani says:
[T]he deracinating effect that registers itself as a condition of enablement insofar as it liberates epistemic possibilities which until now had remained captives of the tyranny of here and now—that is, the knowing subject tethered to a local domain and a privileged frame of reference.[39]
The paradigm of a «conserved relation» between subject and object in the speculative sense is overthrown. The philosophy of armchair philosophers is over. Negarestani goes on to describe the recursive anatomy of the process of ‹localization›:
The question ‹Where is the concept?› demands a methodology for approaching or seeing the concept from a perspective that is adjacent, rather than from a perspective that is fixed upon it. This is by way of a recursive procedure in which we say ‹Where is the concept?› and then we repeat this procedure. In other words, localization (Where?) is combined with recursion. Since localization is an analytico-synthetic procedure that unbinds new alternative addresses for a local site/concept, then repeating localization means that new paths branch from the existing paths. This diffusion of pathways or addresses for a local horizon is registered as a ramified path structure where new alternative addresses and opportunities for local-global synthesis are progressively unfolded. As I argued the concept as a local site is fringed with possibilities of alternative reorientations. The ramified path structure suggests a form of step-wise navigation via these possible reorientations through which the concept is simultaneously studied, traced, revised and constructed. […]
We ask ‹where is x?› then we repeat the question over and over. Every time we localize x, we see or approach it from a new address in the environment in which x is immersed. In our example of a point, the point can be seen not only according to new variable coordinates but also according to different layers of organization. It can be conceived arithmetically, geometrically, algebraically, topologically, and so forth. Accordingly, the operation ‹localization recursion› yields new ramifying paths and in doing so broadens the scope of navigation—that is to say, the constructive passage from the local to the global.
An intuitive way to understand the procedure involved with recursive localization and its imports is as follows: Think of the planet Earth. When we are standing on the surface of the planet, we are occupying a location on its geodetic surface. From a local perspective, the geodetic surface appears to be flat and not curved. While occupying this point on the surface, if we ask ‹where is the earth?›, because of our immediate access to this local point where the global properties are perceived differently (i.e., locally), we would say the earth is a fixed sphere, we might even say it is just a flat surface. However, if we launch a perspective operator—a satellite—into the orbit and take pictures of the planet, upon compiling and integrating these pictures we will notice that the planet is fully mobile and it is spheroid. However, if we repeat this procedure from a broader neighborhood and take new orbital portraits or maps of the planet, then we will observe that not only is Earth spheroid, but also it is located within a celestial system held together by the gravitational force. This is a very intuitive and rather trivial understanding of how the product of localization and recursion works: By localizing the horizon and by way of reverse-engineering it from its orbit (i.e., possibilities of reorientation), rather than from its local fixed coordinates (i.e., information readily available by occupying a local section of it), recursive localization identifies the local horizon according to the site wherein it subsists. But from the perspective of recursive localization, the site is nothing but a cascade of ramifying paths and addresses. It is in the wake of these ramifying paths that the characterization of the local, its problems, imports and implications become a matter of navigation—that is to say, analysis and synthesis, remapping and reorientation, revision and construction.[40]
«Recursive localization» becomes a process of «ramification» and «navigation.» Through identifying the horizon of my locale, one is able to «reverse-engineer» the pathways possible from my address of the setting (i.e., from the restricted and bounded information of a local site) and identify more and more global contexts and addresses to conceptualize my locale. A good example, as Negarestani explains in a video, is the Möbius Strip that locally appears one way but globally another (it has only one side).[41] Another example would be a torus, where locally, the surface appears to resemble the space of R² the real number system, but if we zoom out, it actually appears to be a donut, which has certain homological properties different than a sphere, which is locally homeomorphic to R² (i.e., it has two ‹holes› from the homology group ℤ ⊕ ℤ).
The Poincaré-Hopf Theorem relates local behavior of some differentiable object, namely C^∞
vector fields, to the global topological structure of the manifold. Numerous theorems of this general type, relating local invariants to global structure, have been discovered. These form a large but unified subject called global differential geometry or differential topology.[42]
It is important for epistemology to integrate all of these different scales into a synthetic navigation of the landscape. If one were to abide by classical notions of subjectivity, one would be still living in the paradigm of a «flat earth» because of the tyranny of a fixed point. The epistemology that is restricted to a local domain and abuses this framework is also the culprit behind why humans thought the universe was geocentric (as opposed to heliocentric), as there was not enough information from a more universal context.
*Excerpt from Prolegomenon to a Treatise byEric Schmid published by Bauer Verlag, 2022 http://bauerverlag.eu
0. Wilfrid Sellars, «Philosophy and the Scientific Image of Man,» in In the Space of Reasons, eds. Robert B. Brandom and Kevin Scharp (Cambridge: Harvard University Press, 2007), 374.
1. Ibid.
2. Ibid., 388.
3. Ibid., 400.
4. Ibid., 408.
5. Willem deVries, «Wilfrid Sellars,» The Stanford Encyclopedia of Philosophy, accessed July 28, 2021, https://plato.stanford.edu/archives/fall2021/entries/sellars/.
6. «Extensional and intensional definitions,» Wikipedia, accessed July 28, 2021, https://en.wikipedia.org/wiki/Extensional_and_intensional_definitions.
7. See Jean Petitot, «Local/Global,» in Enciclopedia Einaudi 4 (Lisbon: Impresa Nacional, 1986).
8. See Gilles Châtelet, Figuring Space: Philosophy, Mathematics, and Physics (Dordrecht: Kluwer, 2000).
9. Reza Negarestani, «Where is the Concept?,» in When Site Lost the Plot, ed. Robin Mackay (Falmouth: Urbanomic, 2013), 230–231.
10. Pierre Cartier, «Claude Chevalley,» Notices of the American Mathematical Society 31, no. 7 (November 1984): 775.
11. «Relativity of simultaneity,» Wikipedia, accessed July 28, 2021, https://en.wikipedia.org/wiki/Relativity_of_simultaneity.
12. Ray Brassier, «Axiomatic Heresy: The Non-Philosophy of François Laruelle,» Radical Philosophy 121 (September/October 2003): 34.
13. See Stewart Shapiro, Philosophy of Mathematics: Structure and Ontology (Oxford University Press, 1997).
14. Reza Negarestani (@NegarestaniReza), «No, atoms are not entities in the way we use that term in colloquial or traditional philosophical sense. I highly suggest the text that van Fraassen wrote on whether electrons are real or not,» Twitter, February 14, 2020, https://twitter.com/NegarestaniReza/status/1228459131419471882.
15. Geoffrey Hellman and Stewart Shapiro, Mathematical Structuralism (Cambridge University Press, 2018), 2.
16. See Erich Reck and Georg Schiemer, «Structuralism in the Philosophy of Mathematics,» Stanford Encyclopedia of Philosophy, accessed July 28, 2021, https://plato.stanford.edu/entries/structuralism-mathematics/, «However, there is also an important difference between standard if-then-ism and a category-theoretic approach in terms of the ontological commitments involved, as Awodey points out. According to standard if-then-ism, any mathematical statement can be translated into a universally quantified conditional statement, where the quantifiers are effectively meta-theoretic in nature, ranging over all set-theoretic systems of the right type. As such, the approach presupposes a rich ontology of sets in which such systems can be constructed. In contrast, along category-theoretic lines mathematical theorems do not involve such ontological commitments. There is no implicit generalization over the Bourbaki structures of a theory, e.g., over all groups, rings, or number systems. Rather, a mathematical theorem is ‹a schematic statement about a structure […] which can have various instances›. These instances remain undetermined on purpose, unless a further specification of them is needed for the proof of the theorem in question.»
17. See ibid., «A rejoinder should be added, however. McLarty’s and Awodey’s claim that all mathematical properties expressible in categorical set theory are isomorphism invariant has been contested, e.g., in Tsementzis (2017). In fact, Tsementzis argues that neither ZFC nor ETCS provide fully structuralist foundations for mathematics, since their respective languages do not, after all, exclusively allow for the formulation of invariant properties. Then again, both Makkai’s FOLDS system (Makkai 1995, Other Internet Resources, 1998) and the Univalent Foundations program developed in homotopy type theory (Univalent Foundations Program 2013) seem to meet this condition.»
18. See James Ladyman and Stuart Presnell, «Does Homotopy Type Theory Provide a Foundation for Mathematics?,» British Journal for the Philosophy of Science 69, no. 2 (June 2018).
19. See James Ladyman and Stuart Presnell, «A Primer on Homotopy Type Theory Part 1: The Formal Type Theory« (Unpublished manuscript, University of Pittsburgh, 2014), 22, http://philsci-archive.pitt.edu/11157/1/HTT_Primer-PART-1.pdf, «Essentially, we are assuming that the mathematics founded in constructive logic that we study is no worse off as regards ontological questions than any other branch of mathematics on any other foundation. Further, we assume that whatever solutions can be found to philosophical problems regarding ontology of mathematics in other settings can equally well be applied here, in a way that is compatible with the foundational assumptions we’ve made. Homotopy type theory fits particularly well with structuralism in the philosophy of mathematics (see Steve Awodey ‹Structuralism, Invariance and Univalence›) but we do not pursue this in the present work.»
20. Giuseppe Longo, «The Constructed Objectivity of Mathematics and the Cognitive Subject,» in Quantum mechanics, mathematics, cognition and action. Proposals for a formalized epistemology, eds. Mugur-Schachter Mioara and Alwyn Johannes van der Merwe (Cham: Springer Nature, 2003), 433–463.
21. Alexander Boland, personal website, accessed April 21, 2021, https://alexbo.land/.
22. Fernando Zalamea, «Multilayered Sites and Dynamic Logics for Transits between Art and Mathematics,» Glass Bead, Site 0: Castalia, The Game Of Ends And Means (2016): 13, https://www.glass-bead.org/wp-content/uploads/multilayered-sites-and-dynamic-logics-for-transits-between-art-and-mathematics_en.pdf.
23. See Alain Connes and Caterina Consani, «The Arithmetic Site,» Comopte Rendus – Mathematique 352, no. 12 (December 2014).
24. Jean-Pierre Marquis, «Category Theory,» Stanford Encyclopedia of Philosophy, accessed July 27, 2021, https://plato.stanford.edu/entries/category-theory/.
25. John Stillwell, Concise History of Mathematics for Philosophers (Cambridge University Press, 2019), 51.
26. Ibid., 62.
27. Sara Negri, «Kripke completeness revisited,» in Acts of Knowledge: History, Philosophy and Logic, ed. Giuseppe Primiero (Rickmansworth: College Publications, 2009), 237.
28. «Kripke-Joyal semantics,» Wikipedia, accessed July 18, 2021, https://en.wikipedia.org/wiki/Kripke_semantics#Kripke%E2%80%93Joyal_semantics.
29. Fernando Zalamea, «An Elementary Peircean and Category-Theoretic Reading of Being and Event, Logics of Worlds, and The Immanence of Truths,» Filozofski Vestnik 41, no. 2 (2020): 400.
30. See Luc Illusie, «What is a topos?,» Notices of the American Mathematical Society 51, no. 9 (October 2004): 1060, «To give a topology (sometimes called a Grothendieck topology) on C means to specify, for each object U of C, families of maps (Ui –> U)i?I, called covering families, enjoying properties analogous to those of open covers of an open subset of a topological space, such as stability under base change and composition. Once a topology has been chosen on C, C is called a site, and one can define a sheaf of sets on C in the same way as in the case in which C is the category of open subsets of a topological space: a sheaf of sets E on C is a contravariant functor U ? E(U) on C (with values in the category of sets) having the property that for any covering family (Ui ? U)i?I, a section s of E on U, i. e., an element of E(U), can be identified via the «restriction» maps with a family of sections si of E on the Ui’s that coincide on the «intersections» Ui ×U Uj. A topos T is a category equivalent to the category of sheaves of sets on a site C (which is then called a defining site for T).»
31. Fernando Zalamea, «Multilayered Sites and Dynamic Logics for Transits between Art and Mathematics,» Glass Bead, Site 0: Castalia, The Game Of Ends And Means (2016), https://www.glass-bead.org/wp-content/uploads/multilayered-sites-and-dynamic-logics-for-transits-between-art-and-mathematics_en.pdf.
32. «Talk:Sheaf (mathematics),» Wikipedia, accessed July 28, 2021, https://en.wikipedia.org/wiki?title=Talk:Sheaf_(mathematics)#Some_visualization.
33. Ibid.
34. Ibid.
35. Reza Negarestani, «Where is the Concept?,» in When Site Lost the Plot, ed. Robin Mackay (Falmouth: Urbanomic, 2013), 231–233.
36. See Peter Tsatsanis, «On René Thom’s Significance For Mathematics And Philosophy,» Scripta Philosophiæ Naturalis 2 (2012): 213–229.
37. Brian Resnick, «Scientists warn we may need to live with social distancing for a year or more,» Vox, March 17, 2020, https://www.vox.com/science-and-health/2020/3/17/21181694/coronavirus-covid-19-lockdowns-end-how-long-months-years.
38. «Catastrophe theory,» Encyclopedia Britannica, accessed March 9, 2022, https://www.britannica.com/science/catastrophe-theory-mathematics.
39. Reza Negarestani, «Where is the Concept?,» in When Site Lost the Plot, ed. Robin Mackay (Falmouth: Urbanomic, 2013), 233.
40. Ibid., 242–243.
41. «Reza Negarestani interview,» Vimeo, accessed April 2, 2020, https://vimeo.com/271301170.
42. Theodore W. Gamelin and Robert Everist Greene, Introduction to Topology (Mineola, New York: Dover Publications, Inc., 1999), 188.

